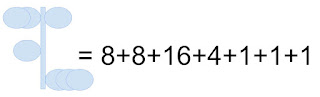Experimental prehistory & various digressions: 2019

The Yupana is also a handy tool for divisions.

There is a way to compute divisions with a Yupana, without any previous knowledge (almost) : no multiplication table, no division table.

If you use the classic interpretation for the yupana (1/2/3/5; sometimes labeled as Mendizabal's interpretation), the one basic thing that is useful to know is "10 = 5+3+2". Also basic and useful : "5=3+2", "3=2+1", "2=1+1" 😉

Illustrations here, with the classic interpretation of the Yupana 1/2/3/5 :

simple division, with explanations

big division, without explanation

If you use other interpretations of the yupana, it should be doable also, but with other basic notions. Notably for the interpretations of Chirinos, Chirinos-Hayakawa and Mendizabal-Hayakawa.

The process is very "automatic", probably also usable, in its principles, with any type of abacus where seeds are free to be moved everywhere (unlike the Soroban, for instance).

I guess that specialists will consider that this is a very well known process, maybe even the historic definition of the process of division 😊... But, well, for an ignorant like me, it is just perfectly suitable for Yupanas.

Process :

Recursively group seeds of the dividend around each seed of the divisor, in equal numbers.

Actually, the groups are to be made around the seeds of the divisor, or around their locations when multiplied by a power of ten : this depends on the difference between the orders of magnitude of the dividend and divisor.

A step of grouping ends when you can't make bigger (equal) groups, then :

- use the number of seeds of a group (same number for all groups, possibly = 0) as the next (or first) digit of the result,

- get rid of the seeds that were in the groups,

- move the remaining seeds (those of the dividend) one row up,

Repeat a new step of grouping with the remaining seeds that were moved up. Make groups of seeds around the seeds of the divisor [those seeds never move] or around their location when multiplied by a suitable power of 10,

When you think it's enough, after you have at least one digit of the result on the same row as the first digit of the divisor :

- position a decimal separator after the digit that is at the level of the first digit of the divisor,

- consider the remaining seeds [only those of the dividend] as the remainder of the division.

---------------------------------------------------------------------------------------------
Illustration here, with the classic interpretation of the Yupana 1/2/3/5 :

Maybe all that may be eased (less seeds) by using dice instead of seeds. Preferably some pre-Columbian Andean type of dice. Like one of those described here https://www.facebook.com/notes/museo-nacional-de-historia-natural-de-chile/el-ancestral-juego-de-dados-y-oráculo-del-quechucague-o-pichca/10154208849277919/

Found in Machu Pichu

Found in Huaca Tres Palos, Lima

The dice used by the promotors of the "Yupana Inka" may be interesting also, but making such beautiful dice would be a challenge ;

Image from https://www.youtube.com/embed/ZUOG_kTcFc4?start=476 (at 8:02)

2019/02/15 - Notes about the process of division with an abacus :

Wikipedia mentions a less efficient method : "A person can calculate division with an abacus by repeatedly placing the dividend on the abacus, and then subtracting the divisor the offset of each digit in the result, counting the number of divisions possible at each offset."

The History of the Abacus says nothing new (just mirrors our modern pencil and paper method)

The fundamental operations in bead arithmetics (with chinese abacus) : as we can guess about abaci with attached beads, the process has to be more like our modern process with pencil and paper (multiplications and subtractions).

How to do division on the abacus in easy steps : not so easy, requires knowledge of multiplication tables (as in the previous articles); normal... it details the use of a "soroban" (attached bead = limited possibilities).

The Most Promising... "Ancient Computers, Part I, Redisovery",by Steve Stephenson, at https://arxiv.org/ftp/arxiv/papers/1206/1206.4349.pdf

No yupana here, but tactics that may be applied to yupanas (maybe... I have to examine that in detail, and see if it can be done somehow with a yupana).
It mentions techniques where only a very small number of pebbles are needed, the potential of abaci with unattached beads/pebbles, divisions and multiplications without knowledge of tables and very automatic : exactly what we want.
Also in line here : https://ethw.org/Ancient_Computers
And more here : http://sks23cu.blogspot.com/2013/07/links-to-my-book-dvds-ancient-computers.html
And examples on the old Stephen Kent Stephenson's Youtube channel SKS23CU

Herodotos and the abacus may deserve more attention, as the proposed solution for division, at first look, resembles the one used higher with the yupana. Although it mentions subtractions that (in the process we described and tested above) we didn't need to perform (other that automatically remove sets of beads, without thinking).

Roman elementary mathematics doesn't seem helpful about easy automatic divisions.

Matematica Andina - La Yupana offers only to mirror the method we use nowadays for divisions.

Journal of mathematics and culture - volume 5 number 2 offers an article "the incan abacus : a curious couting device" (Molly Leonard and Chery Shakiban) that describes a way to perform multiplications and divisions by first preparing tables of multiples.

That's not very appealing if you try to find an automatic calculation process.
But there is a convincing argument : yupana calculations seem to have been a collaborative process involving 2 persons (quipucamayocs). And this hints for the possibility of them using some complementary and parallel processing, not only double checks.

2019/05/29 - Illustration of the division with a yupana

The basis for the process described earlier is illustrated by Oscar Pacheco Rios in a document dated 1999 "Del Quipu Incaico a la Yupana, El computador Ancestral", around page 57. Found here (at least) : https://www.andesacd.org/wp-content/uploads/2019/02/Del-Quipu-Incaico-a-la-Yupana.pdf

2019/11/29 - El tablero medieval de calculo - Jose Maria Nunez - 2003

http://funes.uniandes.edu.co/1522/1/100_Nuñez2003El_RevEMA.pdf

This article describes a simple process for the division : repeated subtractions, In principle, it is identical to the process I used with the yupana : the "grouping" represents a set of identical subtractions.

2020/07/14 - The process of division perfectly illustrated (with a simple example) on Herbert Apaza youtube channel, in 2015

In its principle, it's exactly the process i described (some years later). In practice, with bigger numbers, i guess we are forced to complicate the process that is used here, to avoid maximum confusion on the board.

Digression....

In this article (oups ! reference lost... but see reference about "schärlig" lower), we read that Europe was still using counting boards for computations, as late as in the XVIII th century.

We can infer that those counting boards were still in use in Europe, at the time of the invasion and conquest of the Inca empire (XVI th century). We should even try to verify if there were European counting boards in use, in Peru, 2 centuries after the Spanish conquest. This should have led to a better comprehension of the yupana. Basically, Europe and the Inca empire were doing the same thing, with not so different kinds of counting boards. Maybe for the Spanish, for the ignorant ones as well as for the learned ones, the yupana was just a counting board : no mystery, nothing deserving much attention, just a variant of what they already knew.

The most annoying / promising hypothesis is that the use of the European counting board may have been taught in Peru during the XVII th and XVIII th centuries. That would have touched only a small percentage of the population, but a non negligible proportion of those who were taught writing and counting, among which some native - or mixed blood - Peruvians. This would suggest a possibility of "discourse contamination" around the yupana.

But this hypothesis doesn't seem very promising, after a few hours of internet search :

1) apparently, already in 1590, "pen and ink" were used by the Spanish, at least for "very difficult computations". A citation from a Jesuit priest, Joseph de Acosta, praises the efficiency of the "Indians" of Peru for very difficult computations that would require that an able calculator use pen and ink.

2) in Spain, books in Spanish, about arithmetics with Arabic numerals, were available... See for instance this short study https://www.iejme.com/download/old-arithmetic-books-mathematics-in-spain-in-the-first-half-of-the-sixteenth-century-5935.pdf comparing five of them, printed in the first half of the sixteenth century, hence before the conquest of the Inca empire. Those 5 books were mostly targeting common people and accountants. At first sight, none of those books seem to make reference to counting tables !

2.1) See for instance, an extract, illustrating multiplications, from a book of commercial arithmetic from Spain (1546) "Suma de arithmetica pratica y de todas mercaderias" ... https://www.maa.org/press/periodicals/convergence/mathematical-treasure-commercial-arithmetic-from-spain-1546

3) The use of counting boards may have been limited to Northern Europe (or may have lasted longer there), because the south of Europe was more favorable of Arabic numeration.... see : https://hal.archives-ouvertes.fr/hal-01465419/document describing a book by Schärlig, about counting boards in Europe. Northern Europe only, with sources mainly from Switzerland and West Germany, but also Flanders (Spanish Netherlands), France (Lyon and Strasbourg) until 1792, England. Southern Europe is said to not have used counting boards, but Arabic numbers, for calculations. [scathing comments - in french - about the book and the author here : https://journals.openedition.org/crm/251... the author is criticized for not knowing how to do (and not doing any) bibliographical research].

My remark : the fascinating aspect of that would be that, for Southern Europeans, Inca and Norther European counting boards would have seemed equally strange and would have prompted the same kind of description: "they moved things on a board and where able to make difficult calculations".

4) Colonial education in South America may never have included counting boards. For example, in Guatemala, 1732, a book for teaching, in primary schools, arithmetical basic operations and resolution of problems in commercial environnements, "Aritmetica practica", written by Juan Joseph Padilla, seems to ignore the counting boards, and uses only the Arabic numeration. see : https://hal.archives-ouvertes.fr/hal-01465419/document. In the introduction, by Luis Radford, it is said to be structured like other "libros de abaci" (books that were not about abaci, but about the use of Arabic numbers) written in Europe at the end of the medieval era and after.

so... we can wonder whether any Spanish of the XVI th or XVII th century had ever seen a counting board before arriving in America... except if they had travelled in Northern Europe... and this could well have happened, as Spanish Netherlands was, with the territories or the ex-Inca empire, components of the Spanish Empire for more than 100 years (according to what i read on Wikipedia) :

- incorporation of the Inca empire from 1532 to 1572,

- existence of Spanish Netherland from 1556 to 1714

so... in theory, there was plenty of time for someone (any learned European or Peruvian) to have seen counting boards in the Netherlands - or elsewhere in Northern Europe - and also have lived some time in Peru and have seen or heard (if not outright invented a legend) about Inca counting boards.

The Chirinos-Hayakawa's Yupana

(I just invented this name, we'll see later if there is another name already in use for that thing)

Reminder about the Yupana

The Yupana, is said to have been a prehispanic counting tool / abacus used in the Inca empire. It is said to have been used, as many counting tools in the world, by moving various types of seeds or calculi on a board. The Inca counting board may have been a 4 column grid - according to one 16th century source, Guaman Poma de Ayala - with each column associated with a number of dots (1, 2, 3, 5). There is no definitive explanation of how to use a Yupana : no living ancestral knowledge, nothing clear (yet) found in historical records, only several modern interpretations and educational experiments in south american schools.

Notes : counting boards were still used in Europe, around the time of the conquest of the Inca empire by the spanish. Although the focus nowadays is set on the Guaman Poma 4 columns Yupana, various other tools are also called Yupana. Those that have been found have a number of cells carved into wood, stone or clay. With so few historical traces, nothing rules out that different types of Yupana / grid / counting board / abacus may have been in use simultaneously, for different purposes, different types of calculations or games. Particularly, as we know that the Inca empire was vast and diverse in cultures, languages and peoples.

Finding an efficient and "prehistoric" way to use a 4 columns Yupana

Important points for a viable interpretation of the yupana: paleo-compatible, efficient, reliable in complex computations, limited knowledge requirements (no multiplication tables), reduced number of manipulations, lower attentional requirements, lower memory requirements, possibility to track back errors.

A novel interpretation for the 4 columns Yupana

(I've not yet thoroughly verified if this interpretation has already been described before)

We can create another functional interpretation of the Yupana by mixing two systems :

the Andres Chirinos Rivera interpretation of the Yupana : basically, each dot in a row has a different value, from 1 to 11;
and a notation - not linked to Yupanas - demonstrated by Hayakawa Yoshinori on his youtube channel (早川吉則) : a notation that allows to blindly calculate, as with an abacus, as would do a computer, by using the successive powers of 2, with a very limited set of basic moves and almost zero knowledge requirements ;

The merge between Chirino's Yupana and Hayakawa's notation gives us a Yupana where :

each dot in a row represents a power of 2 : 1, 2, 4, 8, 16, 32, 64, and even more if we need it for special cases, up to 1024;

(if we needed even more, for special calculations we could increase the number of columns and use a "super-yupana")

each row, represents a power of 10, as required for a base 10 numeration system (Inca);
the first 4 dots in each row (1, 2, 4, 8) are sufficient to note any number in base 10;

3 other dots (16, 32, 64) are commonly used during calculations, particularly during multiplications
the remaining dots (128, 256, 512, 1024) may be useful in special cases;

for instance when we want to use fewer rows to note numbers ;
an example, extreme : 512256 may be noted with only 2 dots, on 2 rows.

The first experimentations show that the system is simple, "paleo-compatible", requires zero knowledge of multiplication tables, and need relatively few manipulations. But a high level of attention is still required from the operator. And there is still no obvious way to keep track of the successive operations, in order to find and correct an error.

Illustration 1 - values of the dots in the first row of the "Chirinos-Hayakawa" Yupana.

Video of a "big" multiplication with the Chirinos-Hayakawa's Yupana

Simpler version : Mendizabal-Hayakawa

I've tried a much simpler version, that could be called the Mendizabal-Hayakawa Yupana. It would give the values 1/2/4/8 to the columns, instead of the values 1/2/3/5.

After some experimentation, this Yupana appears to be easy to use, but the 1/2/3/5 marks in the cells are confusing and facilitate errors. We can still try to find a good reason for keeping those 1/2/3/5 marks in the cells. For instance by focusing on the great interest of the groupings by 2, by 3 and by 5 that occur frequently during calculations and that allow easy simplifications (5x8=40; 5x4=20 ; 3x4 = 12 ; 3x8=24).

Illustration 2 :